Tópicos sobre o PyTorch

Jupyter Notebook disponível em https://github.com/psi5892/exercicios_aula_publico/blob/main/pytorch_topicos/pytorch_topicos.ipynb

No Google Colab, é necessário habilitar o suporte à GPU acessando “Change Runtime Type” e selecionando uma opção com GPU como, por exemplo, a “T4 GPU”.

---

O PyTorch é um dos frameworks mais utilizados para o treinamento de modelos de aprendizado de máquina. A seguir, são listados os seus principais componentes e é mostrado um exemplo evoluindo de um algoritmo adaptativo implementado em NumPy, incorporando componentes do PyTorch um a um, até chegar em uma implementação clássica do algoritmo usando PyTorch.

Antes disso, vamos carregar as bibliotecas necessárias:

import numpy as np
import torch
import matplotlib.pyplot as plt

from scipy import signal
from torch import nn

1. Tensores e operações básicas

• Objetos do tipo torch.Tensor, semelhantes à arrays do NumPy, mas com algumas funções adicionais:

  • Podem ser alocados facilmente na GPU;
  • Possibilidade de cálculo automático de gradientes.

• Ref.: https://pytorch.org/docs/stable/tensors.html

• Podem ser criados a partir de listas do Python:

torch.tensor([2, 3, 4])

tensor([2, 3, 4])

• Atributos de shape e rank semelhantes aos arrays do NumPy:

x = torch.tensor([2, 3, 4])
x.shape

torch.Size([3])

x = torch.tensor([[2, 3, 4]])
x.shape

torch.Size([1, 3])

• Tipo padrão para representação de ponto flutuante é o float32:

x = torch.tensor([[2., 3., 4.]])
x.dtype

torch.float32

• Funções auxiliares para criação de tensores com zeros, uns, aleatórios e matrizes identidade:

torch.zeros((2, 3))

tensor([[0., 0., 0.],
        [0., 0., 0.]])

torch.ones((3, 2))

tensor([[1., 1.],
        [1., 1.],
        [1., 1.]])

torch.rand(2, 2)

tensor([[0.4627, 0.0157],
        [0.7564, 0.2955]])

torch.randn(3, 3)

tensor([[ 0.8184, -0.8506,  0.1130],
        [-0.6483,  0.3056, -1.1019],
        [ 0.2038,  0.0101, -0.0732]])

torch.eye(3)

tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])

• Funções auxiliares para criação de sequências:

torch.linspace(0, 1, 10)

tensor([0.0000, 0.1111, 0.2222, 0.3333, 0.4444, 0.5556, 0.6667, 0.7778, 0.8889,
        1.0000])

torch.arange(10)

tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

• reshapee view: são semelhantes, mas
  • view usa os mesmos dados do tensor original. Não funciona para o caso de dados não contíguos;
  • reshape tenta fazer o mesmo que view, mas no caso de dados não contíguos, retorna um tensor com uma cópia dos dados originais.
• A sugestão é usar sempre view;
• Ref.: https://stackoverflow.com/questions/49643225/whats-the-difference-between-reshape-and-view-in-pytorch

x = torch.rand(4,3)
x

tensor([[0.5454, 0.9074, 0.4452],
        [0.0081, 0.8214, 0.5032],
        [0.5534, 0.5719, 0.6812],
        [0.5485, 0.8859, 0.3083]])

x.view(12, -1)

tensor([[0.5454],
        [0.9074],
        [0.4452],
        [0.0081],
        [0.8214],
        [0.5032],
        [0.5534],
        [0.5719],
        [0.6812],
        [0.5485],
        [0.8859],
        [0.3083]])

x.reshape(12, -1)

tensor([[0.5454],
        [0.9074],
        [0.4452],
        [0.0081],
        [0.8214],
        [0.5032],
        [0.5534],
        [0.5719],
        [0.6812],
        [0.5485],
        [0.8859],
        [0.3083]])

1.1 Operações

• Operações aritméticas e matriciais semelhantes às do NumPy;
• PyTorch disponibiliza diversas operações ponto a ponto como torch.abs() e torch.cos() e diversas operações de redução como torch.sum() e torch.mean();
• É importante utilizar as operações do PyTorch para processar os tensores, para que seja possível calcular o gradiente automaticamente com o autograd;
• Além disso, há diversas operações de comparação, espectrais e outras.
• Referência: https://pytorch.org/docs/stable/torch.html#math-operations

1.2 Alocação em CPU e em GPU

• Atributo is_cuda permite ver se o tensor está alocado na GPU:

x = torch.Tensor([1, 2, 3])

x.is_cuda

False

• Para alocar na GPU, é necessário criar um objeto device e usar o método .to():

device = torch.device("cuda")
x = x.to(device)

x.is_cuda

True

• É possível ver se há GPU disponível com o método torch.cuda.is_available():

torch.cuda.is_available() 

True

• É usual usar a seguinte estrutura para alocação automática de tensores na GPU, quando disponível:

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
x = x.to(device)

• Para trazer realocar um tensor de volta à CPU, pode-se usar .cpu():

x.is_cuda

True

x = x.cpu()

x.is_cuda

False

• O método .to() também é usado para fazer casting de tensores:

x.dtype

torch.float32

y = x.to(torch.float64)
y.dtype

torch.float64

1.3 Conversão de dados para NumPy e vice-versa

• Um tensor do PyTorch pode ser convertido para um array do NumPy usando o método .numpy():

x = torch.randn(5,5)
x

tensor([[-0.6816,  0.0935,  0.2459, -0.7493,  0.3136],
        [-1.2594, -0.5296,  0.8730, -0.7298, -1.5338],
        [-1.8568,  1.3244,  0.6735, -1.0898,  1.5097],
        [ 1.3226,  0.5073, -1.1426, -0.4718,  0.3528],
        [ 0.9534,  0.1328, -1.2758, -0.4226, -0.2927]])

x.dtype

torch.float32

x_np = x.numpy()
x_np

array([[-0.68164784,  0.0934647 ,  0.2458577 , -0.74928635,  0.31357208],
       [-1.2594244 , -0.5295776 ,  0.8729781 , -0.7298177 , -1.5337765 ],
       [-1.8568362 ,  1.3243922 ,  0.67345995, -1.0897577 ,  1.5096619 ],
       [ 1.3226392 ,  0.5072677 , -1.1425856 , -0.471815  ,  0.3528156 ],
       [ 0.9534018 ,  0.1327898 , -1.2757865 , -0.42259562, -0.2927368 ]],
      dtype=float32)

x_np.dtype

dtype('float32')

• torch.Tensor pode criar um tensor PyTorch a partir de um array do NumPy, mas é necessário atenção à precisão numérica:

x_np = np.random.randn(5,5)
x_np

array([[ 1.31432832, -0.36861244, -0.3046562 , -0.33023771, -0.82671593],
       [-0.51243873,  0.72323039,  0.04969584, -0.65471439,  1.55967213],
       [-0.83907024,  0.75255006,  0.79133042, -0.58951383, -0.45952117],
       [-0.11569936, -1.68461198,  0.6804936 , -0.18411678, -0.71627022],
       [ 0.76343194, -1.04045083,  1.82626996,  0.34407146, -0.41066983]])

x_np.dtype

dtype('float64')

x = torch.Tensor(x_np,)
x

tensor([[ 1.3143, -0.3686, -0.3047, -0.3302, -0.8267],
        [-0.5124,  0.7232,  0.0497, -0.6547,  1.5597],
        [-0.8391,  0.7526,  0.7913, -0.5895, -0.4595],
        [-0.1157, -1.6846,  0.6805, -0.1841, -0.7163],
        [ 0.7634, -1.0405,  1.8263,  0.3441, -0.4107]])

x.dtype

torch.float32

• A função torch.from_numpy preserva o tipo do array NumPy:

x2 = torch.from_numpy(x_np)
x2.dtype

torch.float64

2. Autograd

• Tensores com o atributo requires_grad=True têm o gradiente calculado automaticamente;
• Só vetores do tipo float ou complex podem usar requires_grad=True.

x0 = torch.tensor([1., 2., 3.], requires_grad=True)
x0

tensor([1., 2., 3.], requires_grad=True)

x1 = torch.tensor([4., 5., 6.], requires_grad=True)
x1

tensor([4., 5., 6.], requires_grad=True)

• Tensores criados a partir de outros com requires_grad=True também têm requires_grad=True:

f = torch.sum(x0**2 + x1)

f.requires_grad

True

• Tensores criados pelo usuário são leaf nodes no grafo, identificados pelo atributo is_leaf:

x0.is_leaf

True

x1.is_leaf

True

f.is_leaf

False

• Gradiente de f em relação x0 e x1:

\[ \frac{\partial f}{\partial \mathbf{x}} = \left[ \begin{matrix} \frac{\partial f}{\partial x_0}\\ \frac{\partial f}{\partial x_1}\\ \end{matrix} \right] = \left[ \begin{matrix} 2x_0\\ 1\\ \end{matrix} \right] \]

• Os gradientes são armazenados no atributo grad, inicialmente igual a None:

x0.grad is None

True

x1.grad is None

True

• Para que os gradientes sejam calculados, é necessário executar o método .backward() do nó em relação ao qual se deseja calculá-los:

f.backward()

x0.grad

tensor([2., 4., 6.])

x0

tensor([1., 2., 3.], requires_grad=True)

x1.grad

tensor([1., 1., 1.])

x1

tensor([4., 5., 6.], requires_grad=True)

3. Do NumPy ao PyTorch

A seguir, serão apresentados os principais elementos do PyTorch, partindo de um exemplo de treinamento de um modelo com o LMS implementado com o NumPy. Serão abordados:

• Uso de tensores PyTorch;
• Uso do autograd;
• Blocos para função custo;
• Blocos para otimizadores;
• Uso de objetos representando modelos PyTorch;
• Uso de blocos PyTorch para a composição de modelos.

As mudanças no código serão indicadas por comentários.

3.1 Começando pelo NumPy

• Código para treinamento de um modelo com o LMS para identificação de sistemas:

N = 500
M = 3
sigmav2 = 0.01
eta = 0.1

x = np.random.randn(N, 1)
wo = np.array([[0.1, 0.2, 0.3]])
d = signal.lfilter(wo.squeeze(), 1, x.squeeze()) + np.sqrt(sigmav2) * np.random.randn(N)
d = d.reshape(-1, 1)

def lms(x, d, eta, M):
    N = len(x)
    xM = np.zeros((M, 1))
    wi = np.zeros((1, M))    
    y = np.zeros((N, 1))
    e = np.zeros((N, 1))
    w = np.zeros((N + 1, M))
    
    for i in range(N):
        xM = np.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        yi = wi @ xM
        ei = d[i] - yi
        wi = wi + eta/2 * 2 * ei * xM.T
        y[i] = yi
        e[i] = ei
        w[i + 1, :] = wi
    return y, e, w

(y_lms, e_lms, w_lms) = lms(x, d, eta, M)

• Vamos comparar a evolução dos pesos, usando a seguinte função:

def plot_ws(w, w_lms):
    plt.figure()
    plt.plot(w, "b")
    plt.plot(w_lms, "k", linewidth=5, alpha=0.5)
    plt.xlabel("iterações")
    plt.ylabel("coeficientes")
    plt.grid()

plot_ws(w_lms, w_lms)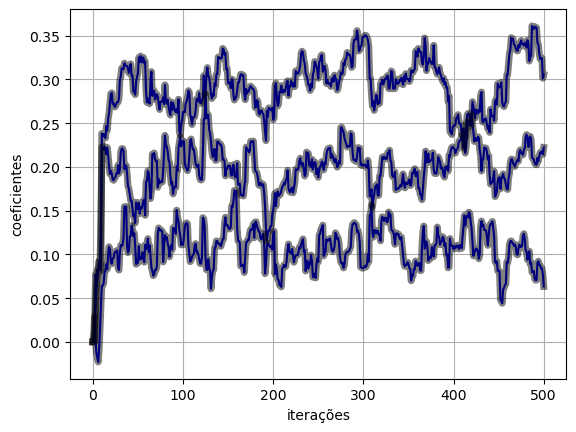

3.2 Uso de tensores PyTorch

• Para manter a precisão numérica padrão do NumPy, vamos configurar o PyTorch para usar tensores do tipo float64:

torch.set_default_dtype(torch.float64)

• A forma de uso dos tensores PyTorch é bem semelhante à dos arrays NumPy. Na maioria dos casos, basta trocar a chamada np. por torch.:

x = torch.tensor(x)
wo = torch.tensor(wo)
d = torch.tensor(d)

def lms_torch(x, d, eta, M):
    N = len(x)
    
    # xM = np.zeros((M, 1))
    # wi = np.zeros((1, M))
    # y = np.zeros((N, 1))
    # e = np.zeros((N, 1))
    # w = np.zeros((N + 1, M))
    xM = torch.zeros((M, 1))
    wi = torch.zeros((1, M))
    y = torch.zeros((N, 1))
    e = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)
    
    for i in range(N):
        
        # xM = np.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        
        yi = wi @ xM
        ei = d[i] - yi
        wi = wi + eta/2 * 2 * ei * xM.T
        y[i] = yi
        e[i] = ei
        w[i + 1, :] = wi
    return y, e, w

(y_torch, e_torch, w_torch) = lms_torch(x, d, eta, M)

plot_ws(w_torch.numpy(), w_lms)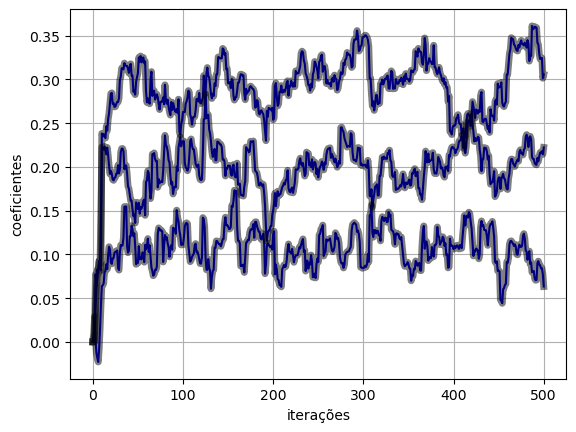

3.3 Uso do autograd

• Tensores que necessitam do cálculo do gradiente, devem ter o atributo requires_grad=True;
• Gradientes são calculados utilizando o método .backward() chamado no objeto que representa o nó em relação ao qual desejamos calcular os gradientes;
• É necessário tomar cuidado com operações para as quais não queremos calcular o gradiente. Nesses casos, utilizamos o bloco de contexto with torch.no_grad():;
• Note que é importante não sobrescrever o objeto wi para que os gradientes sejam computados corretamente (uso de wi[:] = (...));
• A cada chamada de .backward(), os valores dos gradientes são acumulados nos atributos .grad de cada parâmetro do modelo;
  • Dessa forma, é necessário zerar os gradientes a cada iteração, usando o método .grad.zero_().

def lms_torch_autograd(x, d, eta, M):
    N = len(x)
    xM = torch.zeros((M, 1))

    # wi = torch.zeros((1, M))
    wi = torch.zeros((1, M), requires_grad=True)

    y = torch.zeros((N, 1))
    e = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        yi = wi @ xM
        ei = d[i] - yi        

        # Novo
        mse = ei**2
        mse.backward()

        # wi = wi + eta/2 * 2 * ei * xM.T
        # y[i] = yi
        # e[i] = ei
        # w[i + 1, :] = wi
        with torch.no_grad():            
            wi[:] = wi[:] - eta/2 * wi.grad
            y[i] = yi
            e[i] = ei
            w[i + 1, :] = wi

        # Novo    
        wi.grad.zero_()
        
    return y, e, w

(y_torch_autograd, e_torch_autograd, w_torch_autograd) = lms_torch_autograd(x, d, eta, M)

plot_ws(w_torch_autograd.numpy(), w_lms)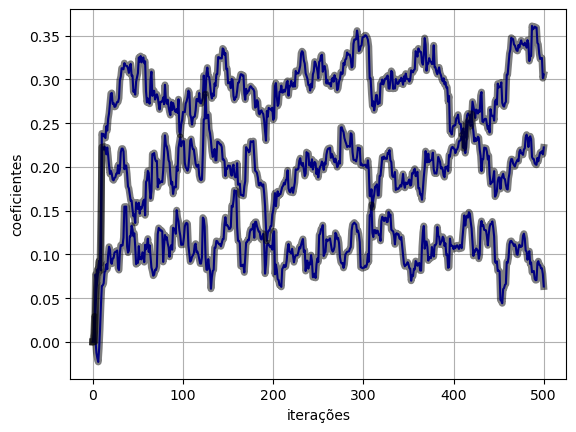

3.4 Blocos para função custo

• O PyTorch disponibiliza diversos blocos para a representação de funções custo: https://pytorch.org/docs/stable/nn.html#loss-functions;
• Para o caso da função custo MSE, utilizamos o bloco nn.MSELoss.

def lms_torch_loss(x, d, eta, M):
    N = len(x)
    xM = torch.zeros((M, 1))
    wi = torch.zeros((1, M), requires_grad=True)
    y = torch.zeros((N, 1))
    
    #e = torch.zeros((N, 1))
    losses = torch.zeros((N, 1))

    w = torch.zeros(N + 1, M)

    # Novo
    loss_function = nn.MSELoss()
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        yi = wi @ xM

        #ei = d[i] - yi
        #mse = ei**2
        #mse.backward()
        loss = loss_function(yi.squeeze(), d[i].squeeze())
        loss.backward()
    
        with torch.no_grad():            
            wi[:] = wi[:] - eta/2 * wi.grad
            y[i] = yi
            losses[i] = loss
            w[i + 1, :] = wi
        wi.grad.zero_()
    return y, loss, w

(y_torch_loss, e_torch_loss, w_torch_loss) = lms_torch_loss(x, d, eta, M)

plot_ws(w_torch_loss.numpy(), w_lms)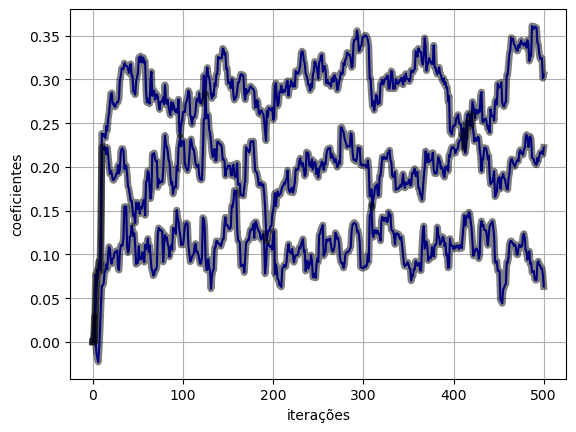

3.5 Blocos para otimizadores

• O PyTorch disponibiliza diversos blocos para a representação de otimizadores: https://pytorch.org/docs/stable/optim.html#algorithms;
• Para o caso do otimizador com o algoritmo backpropagation tradicional, chamado de Stochastic Gradient Descent, utilizamos o bloco nn.SGD;
• A atualização dos pesos do otimizador é feita chamando o método .step().

def lms_torch_optim(x, d, eta, M):
    N = len(x)
    xM = torch.zeros((M, 1))
    wi = torch.zeros((1, M), requires_grad=True)
    y = torch.zeros((N, 1))
    losses = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)

    loss_function = nn.MSELoss()

    # Novo
    optimizer = torch.optim.SGD([wi], lr=eta/2)
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        yi = wi @ xM
        loss = loss_function(yi.squeeze(), d[i].squeeze())
        loss.backward()

        # Novo
        optimizer.step()
    
        with torch.no_grad():            
            
            # wi[:] = wi[:] - eta/2 * wi.grad
            
            y[i] = yi
            losses[i] = loss
            w[i + 1, :] = wi
        wi.grad.zero_()
    return y, loss, w

(y_torch_optim, e_torch_optim, w_torch_optim) = lms_torch_optim(x, d, eta, M)

plot_ws(w_torch_optim.numpy(), w_lms)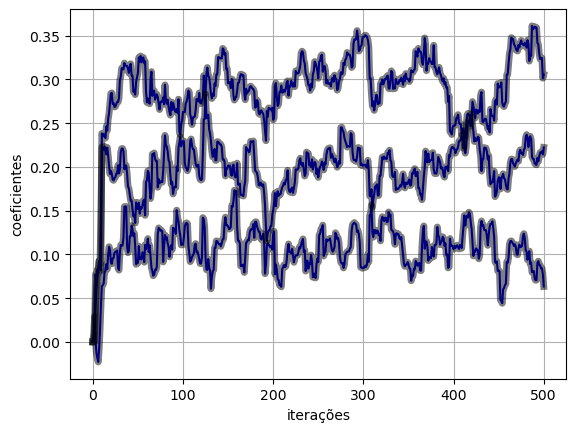

3.6 Uso de objetos representando modelos PyTorch

• Os modelos PyTorch são construídos com a definição de classes que herdam de nn.module;
• No método __init__(), devem ser criados os elementos que compõem o modelo. Nesse caso, vamos utilizar apenas um objeto representando parâmetros genéricos;
• O método forward() define como é calculada a saída a partir da entrada, nesse caso chamada de xM;
• Após a criação da classe, instancia-se um objeto para representar o modelo;
  • A saída do modelo é calculada utilizando este objeto.
• Assim como feito anteriormente, é necessário zerar os gradientes do modelo a cada iteração;
  • É usual fazer isso no início do loop de treinamento.

# Novo
class LMS(nn.Module):
    def __init__(self):
        super().__init__()
        self.wi = nn.Parameter(torch.zeros((1, M), requires_grad=True))
        
    def forward(self, xM):
        output = self.wi @ xM
        return output

# Novo
model = LMS()

# def lms_torch_optim(x, d, eta, M):
def lms_torch_model(x, d, eta, M, model):

    N = len(x)
    xM = torch.zeros((M, 1))
    
    # wi = torch.zeros((1, M), requires_grad=True)
    
    y = torch.zeros((N, 1))
    losses = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)

    loss_function = nn.MSELoss()

    #optimizer = torch.optim.SGD([wi], lr=eta/2)
    optimizer = torch.optim.SGD(model.parameters(), lr=eta/2)
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))

        # yi = wi @ xM
        model.zero_grad()
        yi = model(xM)

        loss = loss_function(yi.squeeze(), d[i].squeeze())
        loss.backward()
        optimizer.step()
    
        with torch.no_grad():            
            y[i] = yi
            losses[i] = loss
            
            # w[i + 1, :] = wi
            w[i + 1, :] = model.wi.clone()

        # wi.grad.zero_()        
    
    return y, loss, w

(y_torch_model, e_torch_model, w_torch_model) = lms_torch_model(x, d, eta, M, model)

plot_ws(w_torch_model.numpy(), w_lms)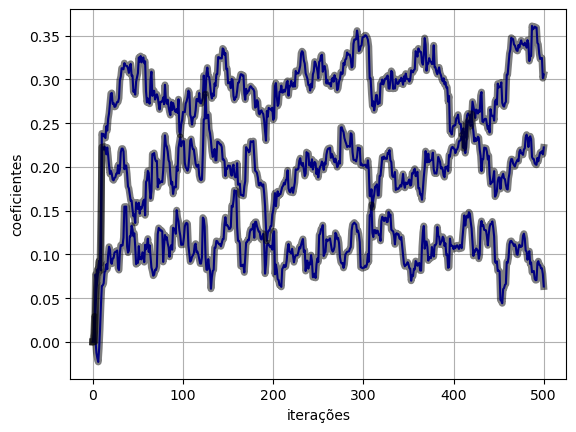

3.7 Uso de blocos PyTorch para a composição de modelos

• No último exemplo, construímos um modelo PyTorch baseado em um conjunto de parâmetros configurados com nn.Parameter.
  • No entanto, o PyTorch conta com inúmeros blocos para a composição de modelos como blocos lineares e funções de ativação para a composição de camadas de redes MLP;
  • Ref.: https://pytorch.org/docs/stable/nn.html.
• No caso do LMS, podemos utilizar o bloco nn.Linear.

# class LMS(nn.Module):
#     def __init__(self):
#         super().__init__()
#         self.wi = nn.Parameter(torch.zeros((1, M), requires_grad=True))
        
#     def forward(self, xM):
#         output = self.wi @ xM
#         return output

class LMS(nn.Module):
    def __init__(self):
        super().__init__()
        self.l1 = nn.Linear(M, 1, bias=False)        
        
    def forward(self, x):
        output = self.l1(x.squeeze())
        return output

model = LMS()

def lms_torch_model_2(x, d, eta, M, model):
    N = len(x)
    xM = torch.zeros((M, 1))
    y = torch.zeros((N, 1))
    losses = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)

    loss_function = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=eta/2)
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        model.zero_grad()
        yi = model(xM)
        loss = loss_function(yi.squeeze(), d[i].squeeze())
        loss.backward()
        optimizer.step()
    
        with torch.no_grad():            
            y[i] = yi
            losses[i] = loss

            # w[i + 1, :] = model.wi.clone()
            w[i + 1, :] = model.l1.weight.clone()

    return y, loss, w

(y_torch_model_2, e_torch_model_2, w_torch_model_2) = lms_torch_model_2(x, d, eta, M, model)

plot_ws(w_torch_model_2.numpy(), w_lms)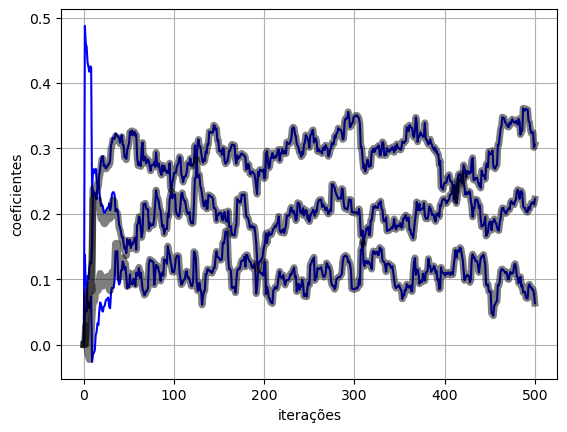

• As curvas de evolução dos pesos não coincidem com as anteriores, neste caso.
  • Isso ocorre por conta da inicialialização dos pesos utilizada pelo bloco nn.Linearque não são inicializados com zeros, conforme descrito na documentação.
• Para obter o mesmo comportamento, é necessário inicializar os pesos com zeros:

class LMS(nn.Module):
    def __init__(self):
        super().__init__()
        self.l1 = nn.Linear(M, 1, bias=False)

    def forward(self, x):
        output = self.l1(x.squeeze())
        return output

# Novo
def weights_init(m):
    classname = m.__class__.__name__    
    if classname.find('Linear') != -1:
        if m.weight is not None:
            #torch.nn.init.xavier_normal_(m.weight)
            torch.nn.init.zeros_(m.weight)
        if m.bias is not None:
            torch.nn.init.zeros_(m.bias)

model = LMS()

# Novo
model.apply(weights_init)


def lms_torch_model_3(x, d, eta, M, model):
    N = len(x)
    xM = torch.zeros((M, 1))
    y = torch.zeros((N, 1))
    losses = torch.zeros((N, 1))
    w = torch.zeros(N + 1, M)

    loss_function = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=eta/2)
    
    for i in range(N):
        xM = torch.vstack((x[i : i + 1, [0]], xM[0 : M - 1, [0]]))
        model.zero_grad()
        yi = model(xM)
        loss = loss_function(yi.squeeze(), d[i].squeeze())
        loss.backward()
        optimizer.step()
    
        with torch.no_grad():            
            y[i] = yi
            losses[i] = loss            
            w[i + 1, :] = model.l1.weight.clone()
    return y, loss, w

(y_torch_model_3, e_torch_model_3, w_torch_model_3) = lms_torch_model_3(x, d, eta, M, model)

plot_ws(w_torch_model_3.numpy(), w_lms)