Análise de Discriminantes Lineares
\[ \newcommand{\Her}{\scriptscriptstyle H} \newcommand{\T}{\rm T} %\newcommand{\R}{\scriptscriptstyle R} \newcommand{\I}{\scriptscriptstyle I} \newcommand{\mT}{\scriptscriptstyle -T} \newcommand{\vir}{,\hspace{-0.15ex}} \newcommand{\M}{\scriptscriptstyle M} \newcommand{\RNN}{\rm \scriptscriptstyle RNN} \newcommand{\E}{{\rm E}} \newcommand{\uM}{{\mathbf u}} \newcommand{\aM}{{\mathbf a}} \newcommand{\bM}{{\mathbf b}} \newcommand{\cM}{{\mathbf c}} \newcommand{\sM}{{\mathbf s}} \newcommand{\SM}{{\mathbf S}} \newcommand{\vM}{{\mathbf v}} \newcommand{\UM}{{\mathbf U}} \newcommand{\VM}{{\mathbf V}} \newcommand{\RM}{{\mathbf R}} \newcommand{\DM}{{\mathbf D}} \newcommand{\PM}{{\mathbf P}} \newcommand{\HM}{{\mathbf H}} \newcommand{\LM}{{\mathbf L}} \newcommand{\AM}{{\mathbf A}} \newcommand{\FM}{{\mathbf F}} \newcommand{\BM}{{\mathbf B}} \newcommand{\QM}{{\mathbf Q}} \newcommand{\SigmaM}{{\boldsymbol{\Sigma}}} \newcommand{\IM}{{\mathbf I}} \newcommand{\JM}{{\mathbf J}} \newcommand{\yM}{{\mathbf y}} \newcommand{\yhM}{\hat{\mathbf y}} \newcommand{\xhM}{\hat{\mathbf x}} \newcommand{\zM}{{\mathbf z}} \newcommand{\xM}{{\mathbf x}} \newcommand{\eM}{{\mathbf e}} \newcommand{\zeroM}{{\mathbf 0}} \newcommand{\rM}{{\mathbf r}} \newcommand{\w}{{\mathbf w}} \newcommand{\wtil}{\widetilde{\mathbf w}} \newcommand{\Dw}{\boldsymbol{\Delta}{\mathbf w}} \newcommand{\Dewp}{\boldsymbol{\Delta}{\mathbf{\dot{w}}}} \newcommand{\wo}{{\mathbf w}_{\rm o}} \newcommand{\q}{{\mathbf q}} \newcommand{\Nuquad}{\|{\mathbf u(n)}\|^2} \newcommand{\traco}{{\rm Tr}} \newcommand{\snum}{\mathbf{s}_{n\!-\!1}} \]
Embora a PCA encontre componentes úteis para representar o conjunto de dados, não há razão para supor que esses componentes são úteis para classificar dados de diferentes classes. Se reunirmos todas as amostras, as direções descartadas pela PCA podem ser exatamente as direções necessárias para distinguir entre as classes. Por exemplo, se tivéssemos dados para as letras maiúsculas impressas O e Q, a PCA pode descobrir as características grosseiras que caracterizam O’s e Q’s, mas pode ignorar a cauda que distingue um O de um Q. Enquanto a PCA busca direções que são eficientes para a representação, a análise de discriminante linear busca direções que são eficientes para discriminação.
A seguir, vamos detalhar essa técnica, começando com o caso particular de duas classes.
Discriminante Linear de Fisher
Vamos começar considerando o problema de projetar um vetor de dados com \(D\) elementos em uma reta. Mesmo que as amostras formassem agrupamentos compactos e bem separados em no espaço de dimensão \(D\), a projeção em uma reta arbitrária geralmente produzirá uma mistura confusa de amostras de todas as classes, o que leva a um desempenho de classificação ruim. No entanto, girando-se a reta, pode-se encontrar uma direção para a qual as amostras projetadas estão bem separadas. Este é exatamente o objetivo da Análise de Discriminante Linear.
Considere um problema de classificação com \(K=2\) classes e um conjunto de dados formado por \(N\) vetores coluna \(\mathbf{x}_n\) de dimensão \(D\times 1\) e elementos reais, ou seja, \(\{\mathbf{x}_n\in \mathbb{R}^{D}\}\), \(n=1, 2, \ldots, N\). Considere ainda que desses \(N\) vetores, há \(N_1\) vetores no subconjunto \({\cal D}_1\) rotulados como pertencentes à classe \(C_1\) e \(N_2\) vetores no subconjunto \({\cal D}_2\) rotulados como pertencentes à classe \(C_2\). Uma combinação linear dos componentes do vetor \(\mathbf{x}_n\) leva ao produto escalar
\[ y_n=\mathbf{w}^{\rm T}\mathbf{x}_n. \]
Supondo que \(\|\mathbf{w}\|=1\), cada \(y_n\) é a projeção do correspondente \(\mathbf{x}_n\) na direção de \(\mathbf{w}\). A norma de \(\mathbf{w}\) não tem importância porque ela meramente escalona \(y_n\), mas a sua a direção é importante. Cabe observar que o conjunto das \(N\) amostras \(y_1, y_2, \cdots, y_N\) pode ser dividido em dois subconjuntos \({\cal Y}_1\) e \({\cal Y}_2\), correspondentes às classes \(C_1\) e \(C_2\), respectivamente.
Se as amostras rotuladas como \(C_1\) estão em um agrupamento e as rotuladas como \(C_2\) em outro, deseja-se que as projeções na direção de \(\mathbf{w}\) sejam bem separadas. A Figura~\(\ref{fig:Fisher}\) ilustra o efeito de escolher direções diferentes para \(\mathbf{w}\) em um exemplo bidimensional. Se as distribuições originais forem multimodais e altamente sobrepostas, mesmo o “melhor” \(\mathbf{w}\) pode ser incapaz de fornecer uma separação adequada e, portanto, esse método será de pouca utilidade.
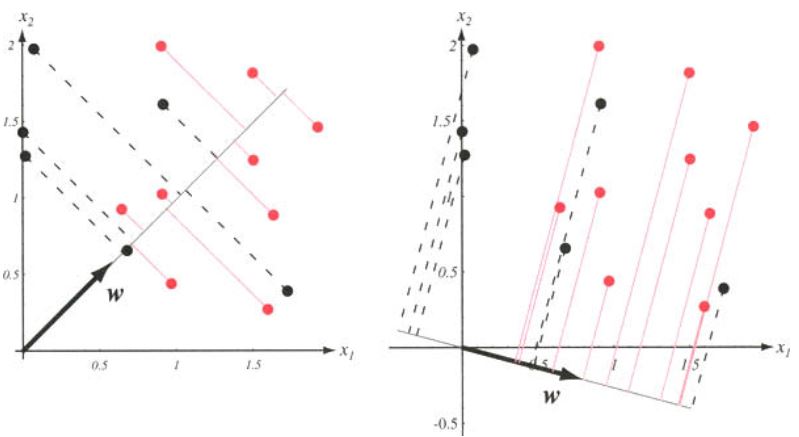
Vamos agora encontrar a melhor direção \(\mathbf{w}\) supondo que seja possível obter uma boa classificação. Uma medida da separação entre as pontos projetados é a diferença entre as médias dos dois subconjuntos. Seja \[ \mathbf{m}_i=\frac{1}{N_i}\sum_{\mathbf{x}\in {\cal D}_i}\mathbf{x} \]
o vetor \(D\times 1\) que representa a média dos dados da classe \(C_i\). Então, a média dos dados projetados da classe \(C_i\) é dada por \[ \widetilde{m}_i=\frac{1}{N_i}\sum_{y\in {\cal Y}_i}y=\frac{1}{N_i}\sum_{\mathbf{x}\in {\cal D}_i}\mathbf{w}^{\rm T}\mathbf{x}=\mathbf{w}^{\rm T}\frac{1}{N_i}\sum_{\mathbf{x}\in {\cal D}_i}\mathbf{x}=\mathbf{w}^{\rm T}\mathbf{m}_i, \]
que corresponde à projeção do vetor \(\mathbf{m}_i\) na direção de \(\mathbf{w}\).
A distância entre as médias projetadas é \[ |\widetilde{m}_1-\widetilde{m}_2|=|\mathbf{w}^{\rm T}(\mathbf{m}_1-\mathbf{m}_2)|. \]
Essa diferença depende da norma de \(\mathbf{w}\) e pode ser tão grande quanto se queira. Para se obter uma boa separação dos dados projetados, desejamos que a diferença entre as médias seja grande e que os dados projetados apresentem uma pequena variação em torno da média de cada classe. Definindo
\[ \widetilde{s}_i^2=\sum_{y\in {\cal Y}_i}(y-\widetilde{m}_i)^2, \]
então \[ \frac{\widetilde{s}_1^2+\widetilde{s}_2^2}{N} \]
é uma estimativa da variância dos dados agrupados e a soma \(\widetilde{s}_1^2+\widetilde{s}_2^2\) é chamada de dispersão total das amostras projetadas dentro da classe (within-class scatter).
O Discriminante Linear de Fisher busca o vetor \(\mathbf{w}\) (independente de sua norma) que maximiza o seguinte critério
\[ J(\mathbf{w})=\frac{(\widetilde{m}_1-\widetilde{m}_2)^2}{\widetilde{s}_1^2+\widetilde{s}_2^2}. \]
Para obter \(J(\cdot)\) como uma função explicita de \(\mathbf{w}\), vamos definir as matrizes de dispersão \(\mathbf{S}_i\) e \(\mathbf{S}_W\), ou seja, \[ \mathbf{S}_i=\sum_{x\in{\cal D}_i}(\mathbf{x}-\mathbf{m}_i)(\mathbf{x}-\mathbf{m}_i)^{\rm T} \]
e \[ \mathbf{S}_{W}=\mathbf{S}_1+\mathbf{S}_2. \]
Então, podemos escrever
\[ \widetilde{s}_i^2=\sum_{x\in{\cal D}_i}(\mathbf{w}^{\rm T}\mathbf{x}-\mathbf{w}^{\rm T}\mathbf{m}_i)^2=\sum_{x\in{\cal D}_i}\mathbf{w}^{\rm T}(\mathbf{x}-\mathbf{m}_i)(\mathbf{x}-\mathbf{m}_i)^{\rm T}\mathbf{w}=\mathbf{w}^{\rm T}\mathbf{S}_i\mathbf{w}. \]
Consequentemente, a dispersão total pode ser escrita como \[ \widetilde{s}_1^2+\widetilde{s}_2^2=\mathbf{w}^{\rm T}\mathbf{S}_W\mathbf{w}. \]
Similarmente, \[ (\widetilde{m}_1-\widetilde{m}_2)^2=(\mathbf{w}^{\rm T}\mathbf{m}_1-\mathbf{w}^{\rm T}\mathbf{m}_2)^2= \mathbf{w}^{\rm T}(\mathbf{m}_1-\mathbf{m}_2)(\mathbf{m}_1-\mathbf{m}_2)^{\T}\mathbf{w}=\mathbf{w}^{\rm T}\mathbf{S}_B\mathbf{w} \]
em que
\[ \mathbf{S}_B\triangleq (\mathbf{m}_1-\mathbf{m}_2)(\mathbf{m}_1-\mathbf{m}_2)^{\T}. \]
A matriz \(\mathbf{S}_W\) é chamada de matriz de dispersão dentro da classe. Ela é proporcional à matriz de covariância dos dados de dimensão \(D\) agrupados. Ela é simétrica e positiva semidefinida, e geralmente é não singular se \(N > D\). Analogamente, \(\mathbf{S}_B\) é chamada de matriz de dispersão entre classes. No entanto, apesar de ser simétrica, por ser o produto externo de dois vetores, seu posto é no máximo um. Em particular, para qualquer \(\mathbf{w}\), \(\mathbf{S}_B\mathbf{w}\) está na direção de \((\mathbf{m}_1-\mathbf{m}_2)\) e \(\mathbf{S}_B\) é singular.
Em termos dessas matrizes, \(J(\mathbf{w})\) pode ser escrito como
\[ J(\mathbf{w})=\frac{\mathbf{w}^{\rm T}\mathbf{S}_B\mathbf{w}}{\mathbf{w}^{\rm T}\mathbf{S}_W\mathbf{w}}, \]
que é conhecida na física matemática como coeficiente de Rayleigh generalizado. O vetor \(\mathbf{w}\) que maximiza \(J(\mathbf{w})\) deve satisfazer o critério \[ \max_{\mathbf{w}\neq \mathbf{0}}\frac{\mathbf{w}^{\rm T}\mathbf{S}_B\mathbf{w}}{\mathbf{w}^{\rm T}\mathbf{S}_W\mathbf{w}}, \]
que é equivalente ao seguinte critério com restrição
\[ \max_{\mathbf{w}\in \mathbb{R}^{D}} \mathbf{w}^{\rm T}\mathbf{S}_B\mathbf{w},\;\;\text{sujeito a}\;\;\mathbf{w}^{\rm T}\mathbf{S}_W\mathbf{w}=1. \]
Para resolver esse critério, podemos usar a técnica de multiplicadores de Lagrange. Assim, obtemos a seguinte função custo
\[ J_{\lambda}(\mathbf{w})=\mathbf{w}^{\rm T}\mathbf{S}_B\mathbf{w}+\lambda(1-\mathbf{w}^{\rm T}\mathbf{S}_W\mathbf{w}). \]
Calculando a derivada em relação \(\mathbf{w}\), obtém-se
\[ \frac{d J_{\lambda}(\mathbf{w})}{d \mathbf{w}}=\mathbf{S}_B\mathbf{w}-\lambda\mathbf{S}_W\mathbf{w}. \]
Igualando essa derivada a zero e se \(\mathbf{S}_{W}\) for não singular, podemos escrever
\[\begin{equation*} \fbox{$\displaystyle \mathbf{S}_{W}^{-1}\mathbf{S}_{B}\mathbf{w}=\lambda \mathbf{w} $} \end{equation*}\]
Assim, \(\mathbf{w}\) é o autovetor relacionado ao único autovalor não nulo, \(\lambda\), da matriz \(\mathbf{S}_{W}^{-1}\mathbf{S}_{B}\). Cabe observar que a matriz \(\mathbf{S}_{W}^{-1}\mathbf{S}_{B}\) continua com posto igual a um e por isso tem um único autovalor não nulo. No caso particular, como \(\mathbf{S}_B\mathbf{w}\) está na direção de \((\mathbf{m}_1-\mathbf{m}_2)\), pode-se calcular \(\mathbf{w}\) como
\[\begin{equation*} \fbox{$\displaystyle \mathbf{w}=\mathbf{S}_{W}^{-1}(\mathbf{m}_1-\mathbf{m}_2). $} \end{equation*}\]
Assim, a classificação foi convertida de um problema \(D\)-dimensional para um problema de classificação em uma dimensão, ou seja, \(K-1\) (quantidade de classes menos um).
Em suma, o Discriminante Linear de Fisher projeta o vetor \(\mathbf{x}\) de dimensão \(D\) em uma dimensão, ou seja, \(y=\mathbf{w}^{\rm T}\mathbf{x}\). Comparando \(y\) com um limiar, este método pode classificar \(\mathbf{x}\) como pertencente à classe \(C_1\) ou à classe \(C_2\). Para esse propósito, \(\mathbf{w}\) deve ser calculado tal que as médias dos dados projetados das duas classes fiquem o mais distante possível uma da outra. Além disso, a variância dos dados projetos de cada classe deve ser a menor possível, o que possibilita uma grande concentração dos dados de cada classe em torno de sua média e a possibilidade de uma classificação correta.
Extensão para mais de duas classes
A Análise de Discriminante Linear (LDA - Linear Discriminant Analysis) é a generalização do Discriminante Linear de Fisher para mais de duas classes (\(K>2\)). Nessa generalização, o vetor \(\mathbf{x}_n\) de dimensão \(D>K\) é projetado no espaço de dimensão \((K-1)\) por meio da transformação
\[ \mathbf{y}_n=\mathbf{W}^{\rm T}\mathbf{x}_n \]
em que
\[ \mathbf{W}=[\mathbf{w}_1\;\mathbf{w}_2\;\cdots\;\mathbf{w}_{K-1}] \]
é uma matriz com dimensões \(D \times (K-1)\), formada por vetores coluna \(\mathbf{w}_k\), \(k=1,2,\cdots, K-1\). Assim, o vetor \(\mathbf{y}_n\) passa a ter a dimensão do número de classes do problema menos um.
Como no Discriminante Linear de Fisher, a LDA busca maximizar a separação entre as classes e ao mesmo tempo reduzir a sobreposição entre elas. Para isso, deve-se estender as definições das matrizes de dispersão entre classes \(\mathbf{S}_B\) e de dispersão dentro das classes \(\mathbf{S}_W\), vistas anteriormente. Assim, obtém-se para o caso de \(K\) classes
\[\begin{align} \mathbf{S}_B&=\sum_{k=1}^{K}N_k(\mathbf{m}_k-\mathbf{m})(\mathbf{m}_k-\mathbf{m})^{\rm T}\nonumber\\ \mathbf{S}_W&=\sum_{k=1}^{K}\sum_{\mathbf{x}\in{\cal D}_i}(\mathbf{x}-\mathbf{m}_i)(\mathbf{x}-\mathbf{m}_i)^{\rm T}\nonumber \end{align}\]
em que
\[ \mathbf{m}=\frac{1}{N}\sum_{n=1}^{N}{\mathbf{x}_n} \]
representa a média global do conjunto de dados. Cabe observar que o termo \((\mathbf{m}_k-\mathbf{m})\) que aparece em \(\mathbf{S}_B\) é o desvio da média de cada classe da média global. Esses desvios formam um conjunto de \(K\) vetores no espaço de características. Entretanto, esses vetores não são independentes. A média global é uma média ponderada das médias das classes, ou seja,
\[ \mathbf{m}=\frac{1}{N}\sum_{k=1}^{K}N_k\mathbf{m}_k. \]
Essa relação introduz uma dependência entre os vetores das \(K\) classes, o que faz com que a matriz \(\mathbf{S}_B\) tenha posto no máximo igual a \(K-1\). Consequentemente, a matriz \(\mathbf{S}_W^{-1}\mathbf{S}_B\) também tem posto no máximo igual a \(K-1\).
A função custo neste caso é dada por
\[ J(\mathbf{W})= \text{Tr}\{(\mathbf{W}^{\rm T} \mathbf{S}_W\mathbf{W})^{-1}(\mathbf{W}^{\rm T} \mathbf{S}_B\mathbf{W})\}, \]
em que \(\text{Tr}\{\cdot\}\) denota o traço de uma matriz. Essa função se reduz à vista anteriormente para \(K=2\). A matriz \(\mathbf{W}\) que maximiza \(J(\mathbf{W})\) é formada pelos autovetores \(\mathbf{w}_k\), \(k=1, 2, \cdots, K-1\) relacionados aos autovalores não nulos de \(\mathbf{S}_W^{-1}\mathbf{S}_B\). Assim, o vetor \(\mathbf{x}_n\) pode ser mapeado em um subespaço de dimensão \((K-1)\) gerado pelos \(K-1\) autovetores correspondentes aos autovalores não nulos. Consequentemente, a otimização de \(J(\mathbf{W})\) produz \(K-1\) características sem perda da classificabilidade. Essas características podem ser consideradas como entrada de um classificador como uma rede neural, o que em geral diminui a dimensionalidade do problema.